【cs231n】图像分类 K最邻近算法 线性分类器
图像分类遇到的问题
- semantic gap 语义鸿沟,人看到的是一张图片,但是计算机看到的是数字矩阵
- viewpoint variation 视角不同,看到的内容不同
- Illumination 照明问题
- Deformation 变形问题
- Occlusion 遮挡问题
- Background Clutter 比如猫身上的条纹和背景很像
- Intraclass variation 类内差异问题,猫有不同的大小颜色等
很难直接写出一个代码来判断他是什么对象

数据驱动的方法
- 收集图片的数据集
- 使用机器学习的方法训练一个分类器
- 在新的图片上来评价这个分类器
K-最近邻算法分类
通过比较图像之间的差异进行分类,通过像素进行比较差异。
首先通过训练函数只是简单地所有的训练数据都记忆下来,每次输入一张图片进行预测时,将遍历已经记忆的训练数据找到最相近的图片,根据最相近的图片的类别来预测这个输入图片的类别。
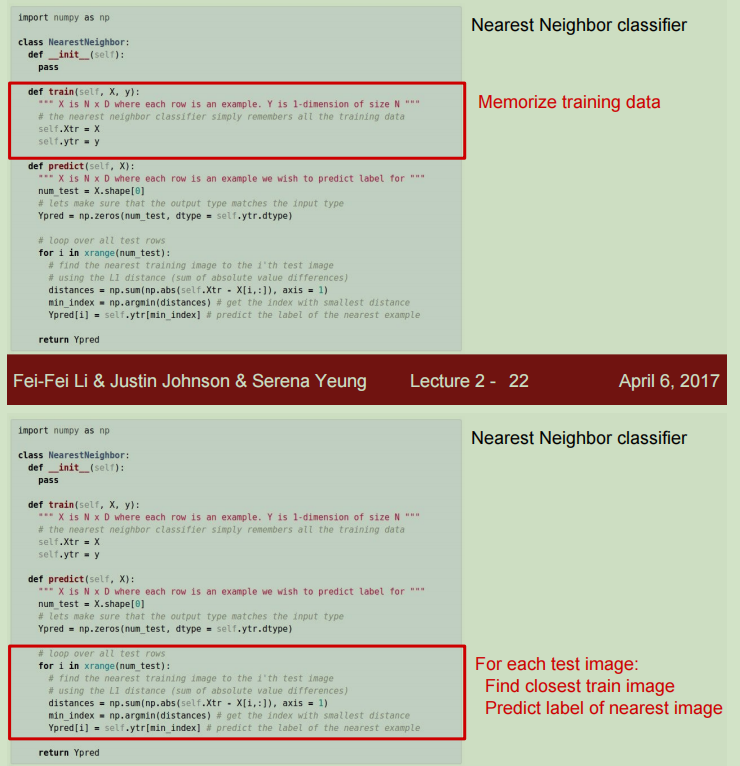
训练的复杂度:O(1)
预测的复杂度:O(N)
这是很坏的一个结果,因为在训练时这个算法很快,但是真正进行预测时很慢,这和我们的初衷完全相反。
K最邻近
如果只计算最邻近一个图片,会有弊端,比如下图,绿色分区中单独有一个黄色的点,因为只计算最近的那个点,所以那一片就会选择黄色的点。
所以K最邻近算法是找到最近的K的点,然后在这些邻近点中进行投票,然后这些票数多的临近点预测出结果,实现这个算法的方式有很多,比如将距离进行加权,但是最简单的还是进行多数投票,临近点中哪个类别最多就确定为哪个类别。
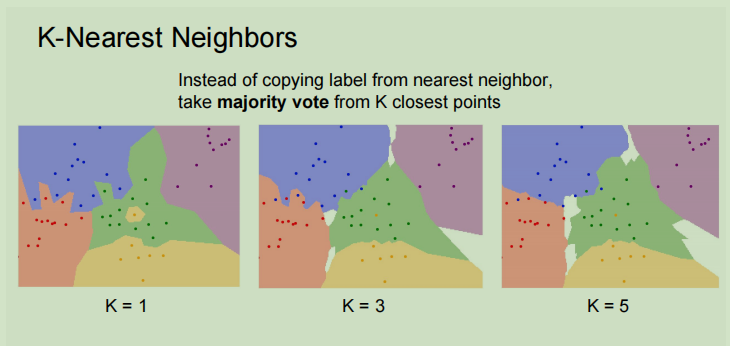
当k=3时,图中的黄色噪点不会导致周围的区域划分为黄色了,决策边界也将随着K的增加而被平滑掉。图中的白色区域代表在这个区域中没有临近点,即没有进行分类。
衡量距离的两种函数
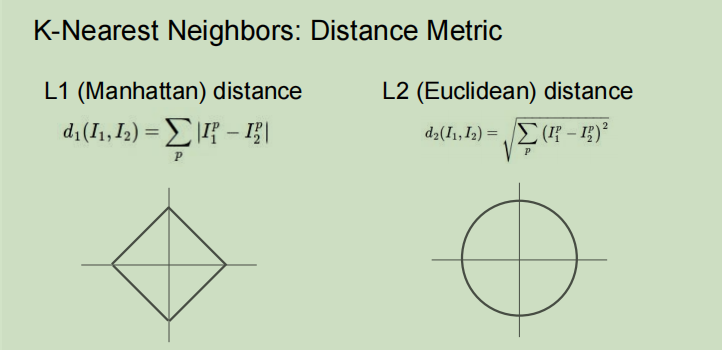
曼哈顿距离(L1)和欧氏距离(L2)
L1距离取决于选取的坐标轴,如果你旋转坐标轴,那么L1距离可能改变,但是L2距离不会改变。所以,如果你输入的向量值有一部分有一些重要的意义,那么L1可能更合适,如果只是空间中的通用向量,没有什么意义,那么L2可能更自然一些。
超参数的确定
超参数:K和距离测量方式
q:什么时候L1比L2好?
a:需要根据实际问题来看,最佳的方法时两种都尝试一下
错误的确定方法:
- 不区分测试集和训练集,总体进行训练选择表现最好的超参数
- 训练之后,在测试集上使用,调参,选取在测试集上表现最好的超参数。坏处:遇到一组新的数据可能不行
正确的做法:
分成三份,训练、验证、测试。在验证数据集上选择合适的超参数,测试数据集最后才能使用
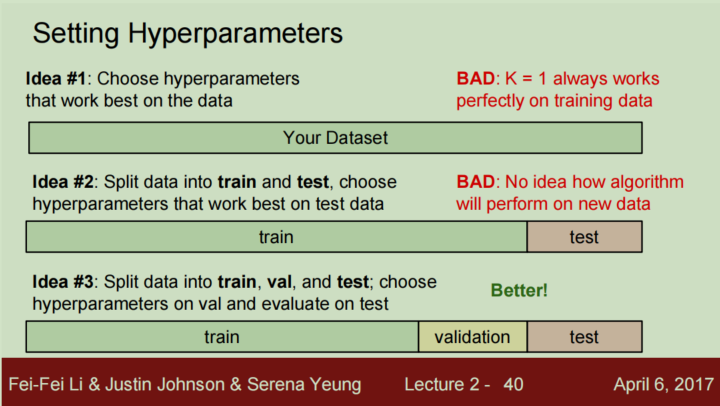
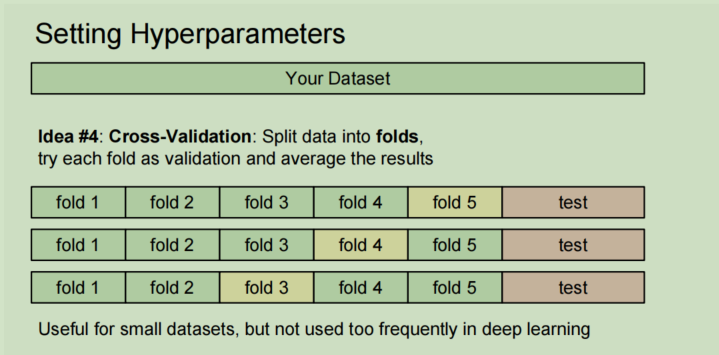
或者使用交叉验证,但是这种方法在深度学习中不是很常用,因为训练数据本身就是很费资源的事情,进行交叉验证需要额外多训练几次,很耗费资源
交叉验证思路就是,分出测试数据集之后的数据平均分成几份,每次选取其中一份作为验证数据集,其余的份数都用来当做训练数据集。这样训练多次,得到最优的参数
测试集是否可以很好地代表现实中的数据?随机将收集来的数据划分为训练集和测试集。
knn不会被使用,它的测试时间很长,使用L1或L2这种向量化的距离衡量方式不适合表示图像之间的视觉相似度,例子:
维度灾难,所需要的样本数呈指数增加
总结:
- 在图片分类中,我们使用训练数据集,训练数据集包括图片和标签,我们需要在测试数据集上预测出图片的标签
- KNN分类器预测标签基于最近的训练样例
- 超参数是,距离的衡量方式和K
- 使用验证数据集来选择超参数,仅在最后使用测试数据集测试模型
线性分类
linear classification
神经网络的模块化
可以把神经网络看成乐高,你可以把不同的神经网络模块组合起来拼接成一个大型卷积网络,线性分类器是深度学习的应用中最基本的构建模块之一。
再例如,该系统输入一幅图像输出对于该图像的描述性句子,工作原理就是使用CNN关注图像处理图像,使用RNN关注语义处理语言,将这两个网络放在一起就可以组成一个很好的处理系统。

线性分类器
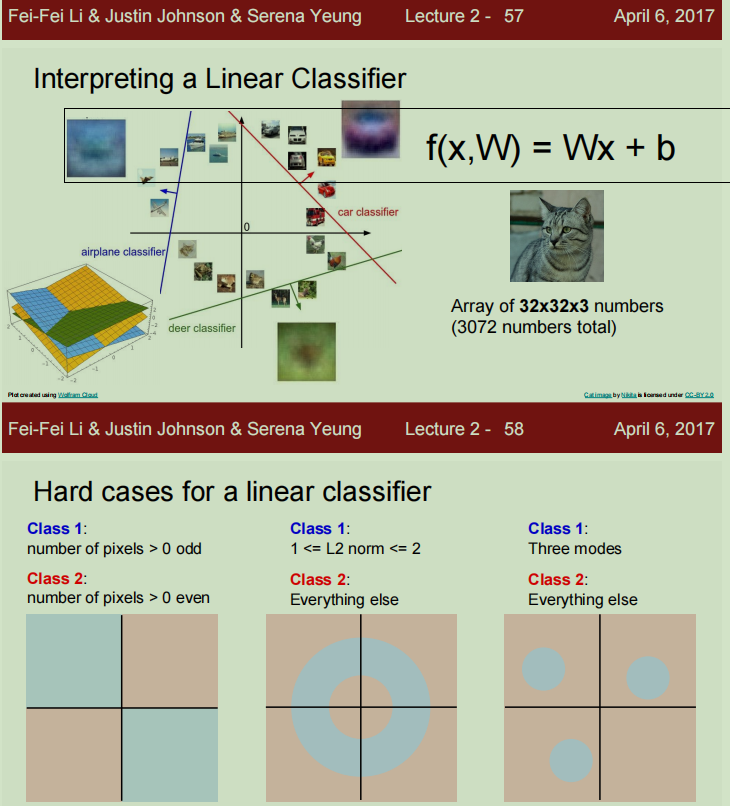
思想就是将图片参数输入,与权重W相乘,可以再加上一个偏差量b(偏差给了数据独立的缩放比例以及每个类别的偏移量),得到一个列向量,每个元素都代表一个类别的得分,该图像所属类别为得分高的那个。原理如下如所示:
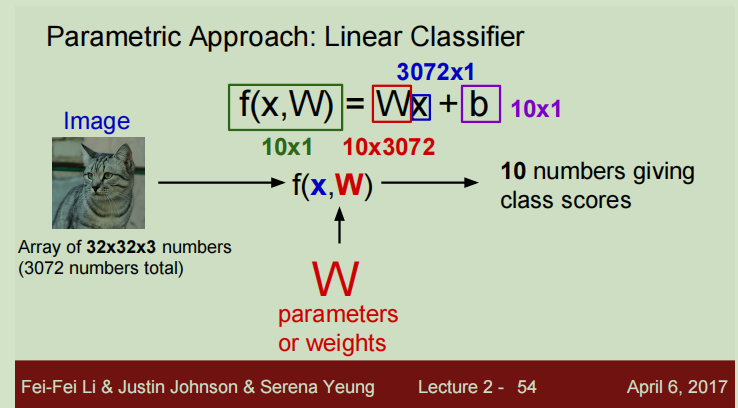
将一个32 32像素三通道的图片看成一个3072的列向量,由于类别一共有10类,那么权重W就可以设置为10 3072的矩阵,那么结果就是一个长度为10的列向量。
具体来看下面这个例子,假设一张像素为4的图片,类别有三类,整个流程如下:
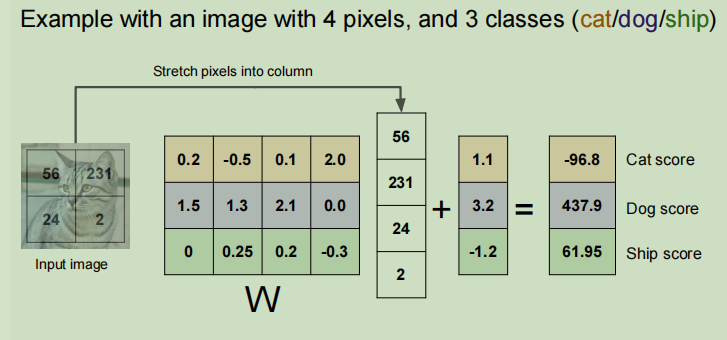
问题来了,那个这个训练好的权重矩阵W到底和输入的图像有什么关系呢?其实可以把权重矩阵的每一行看成一个模板,我们把矩阵中每一行单独拿出来做成一个图像,在CIFAR-10中,训练好的权重矩阵W的每一行对应的图像如下图:

另一种解释:
也可以将每个图片都看成高维空间中的一个点,我们试图通过一条线将每个点进行分类。但是由此而来也会带来线性分类器的困境,当多模态数据出现在不同领域的空间中(比如一个类别出现在不同的领域空间中)