【动手学深度学习】03-感知机
1 感知机
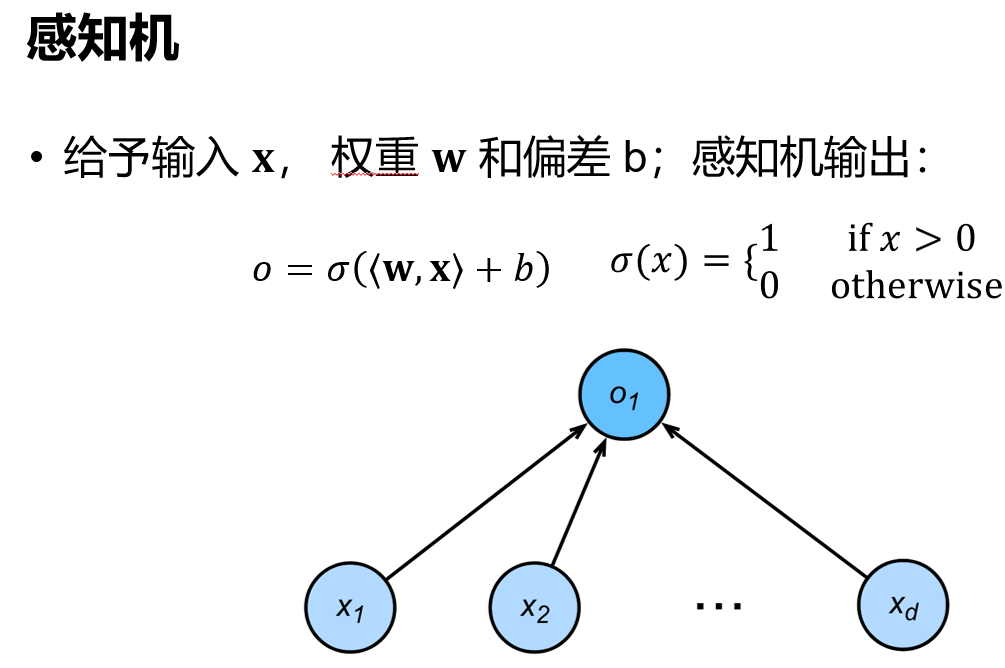
给予输入,权重和偏差,然后感知机输出1或0,其实是个二分类问题
二分类:-1或1
线性回归:输出实数
softmax回归:输出回归概率
1.1 训练感知机
标记$y_i$有值为1和-1,分别对应着二分类中的两个类。如果$< w,x_i >+b$的值小于等于0,即预测的为-1对应的类,但是真实的$y_i$是1,二者相乘结果为非整数表示分类错误,就需要调整参数。
停止条件:如此反复直到所有的数据都分类正确。
等价于使用批量大小为1的梯度下降,每一次拿一个样本去算梯度做更新,不是随机梯度下降是因为感知机是一边又一边的去扫描数据,不是随机取值。损失函数使用max来判断是否分类正确,若正确则取值为0,常数的梯度

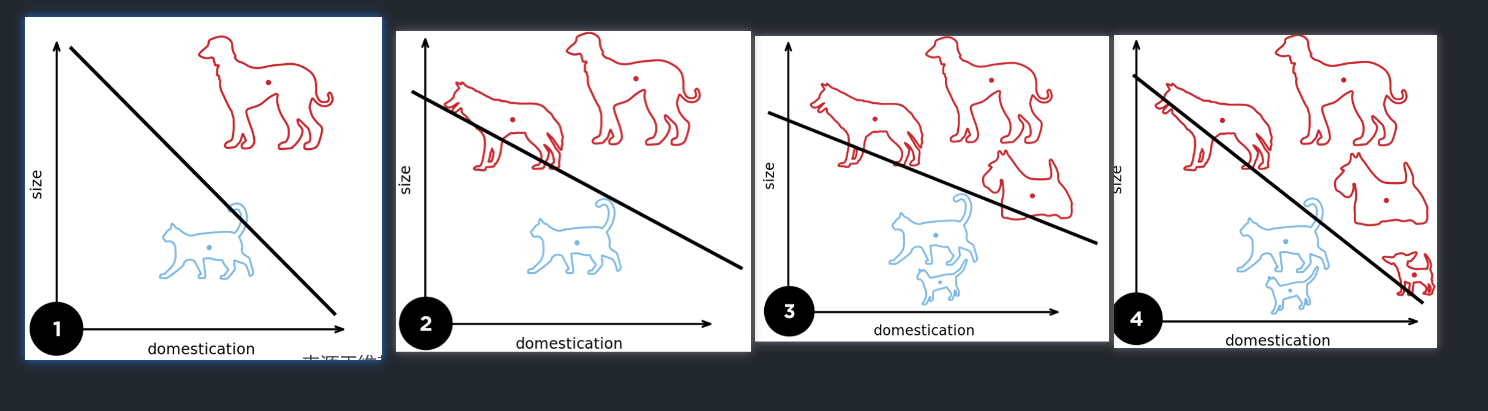
1.2 例子
1.3 收敛定理
暂时不做证明,证明见这里
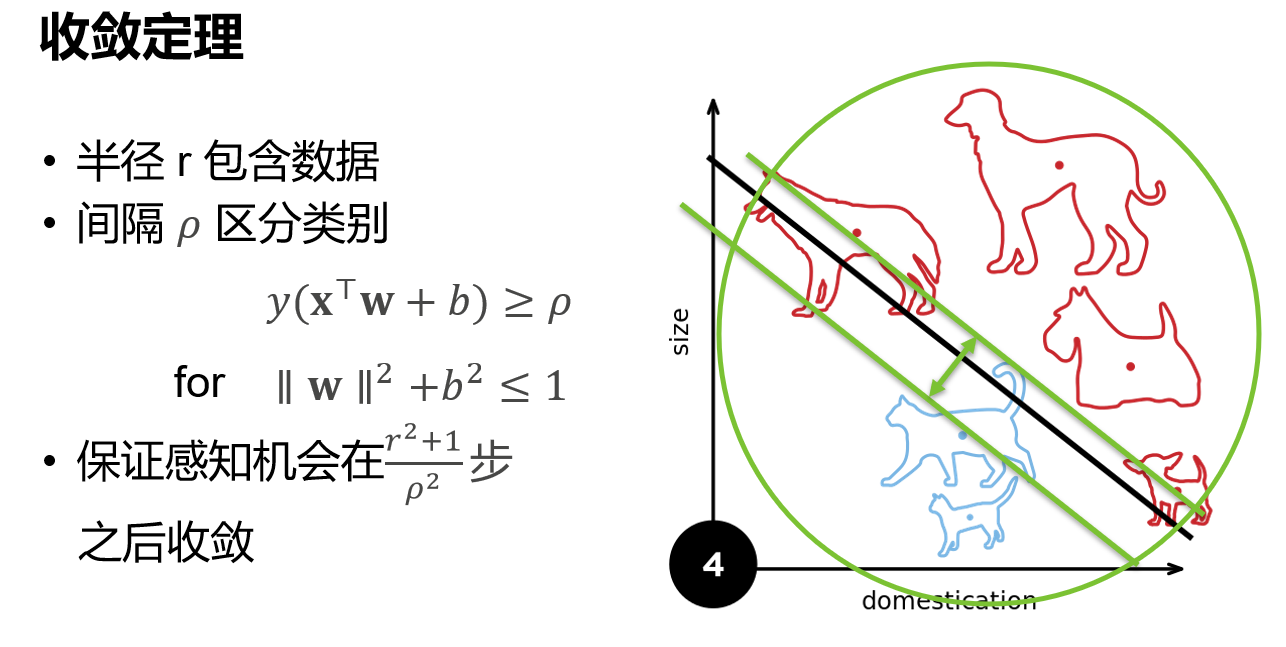
余量ρ使得存在一个分界面,该分界面对于所有的数据都分类正确。
r代表着数据大小,所以收敛的步数与r成正比。ρ是分界面的大小,如果分割面很大,那么就会把数据分类分的很开,就所需要的步数变少,所以步数和ρ成反比。
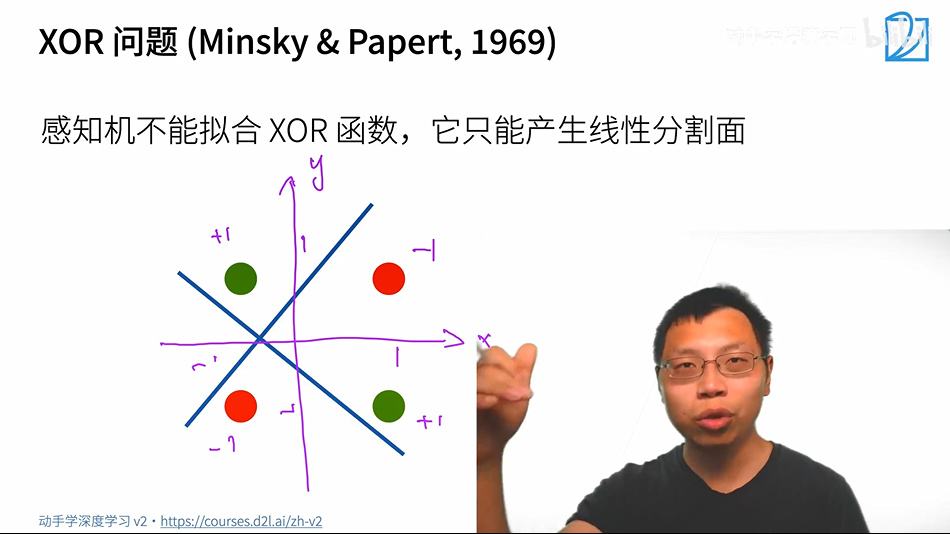
1.4 XOR问题
他只能产生线性分割面,不能拟合XOR函数。该问题直接导致了AI的第一次寒冬。
1.5 总结
- 感知机是一个二等分模型,是最早的AI模型之一
- 它的求解算法等价于使用批量大小为1的梯度下降
- 它不能拟合XOR函数,导致的第一次AI寒冬
2 多层感知机
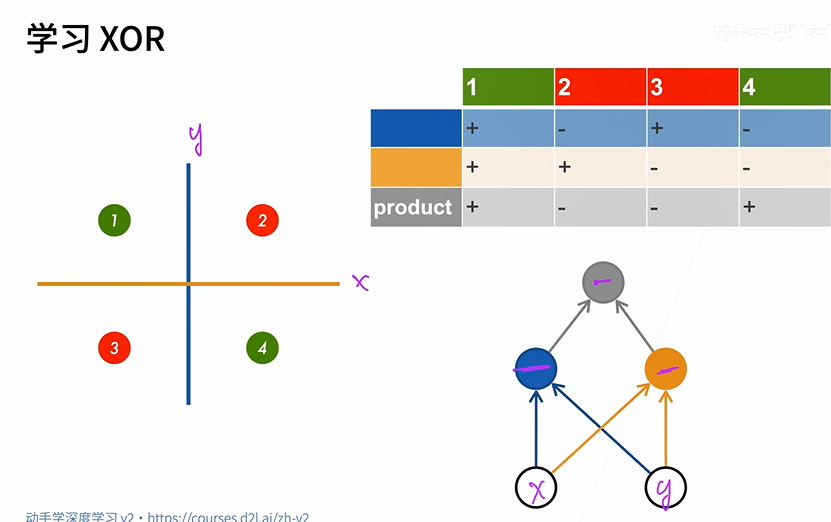
2.1 解决XOR问题
解决XOR问题,单线性模型是不行的,所以使用多层。蓝色的线根据x轴坐标分类,黄色的线根据y轴的坐标分类,之后再把蓝色和黄色的分类结果相乘即可得到正确的分类结果。即如果一个函数解决不了,那就先用几个简单地函数来解决,之后再对简单的函数进行分类解决。
2.2 单隐藏层
隐藏层的大小是超参数。原因:输入的大小是不能改的,输出的大小取决于要分多少类,唯一能够设置的就是超参数的大小。
2.2.1 单类分类
输入:一个n维向量。隐藏层:$W_1$是一个m*n的矩阵,偏移是一个m维的向量。输出层:为一个m维的向量,有多少个分类,就是多少维。
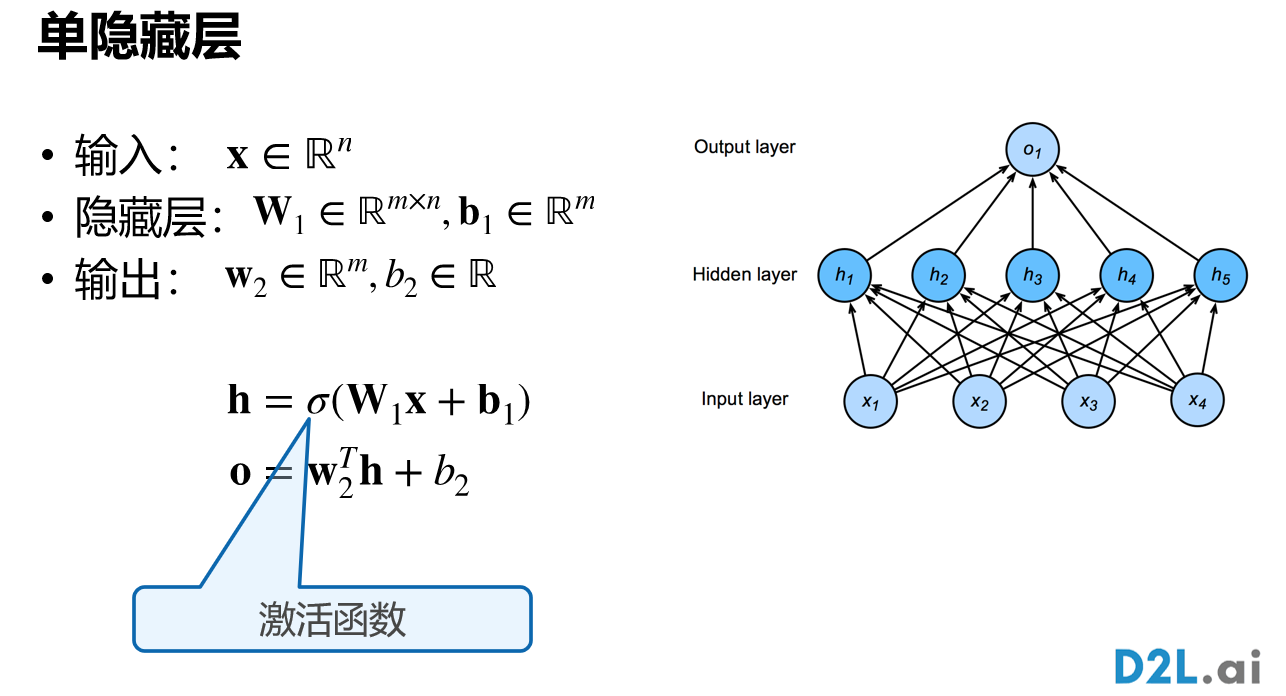
2.2.2 激活函数
函数σ的结果是一个mn的矩阵,该结果作为输入数据到输出层中,再经过输出层的运算得到结果。如果σ是线性的(比如σ=a*x)那么输出层结果是一个线性函数,等价于一个单层的感知机。
sigmoid激活函数:
就是把σ给软化了
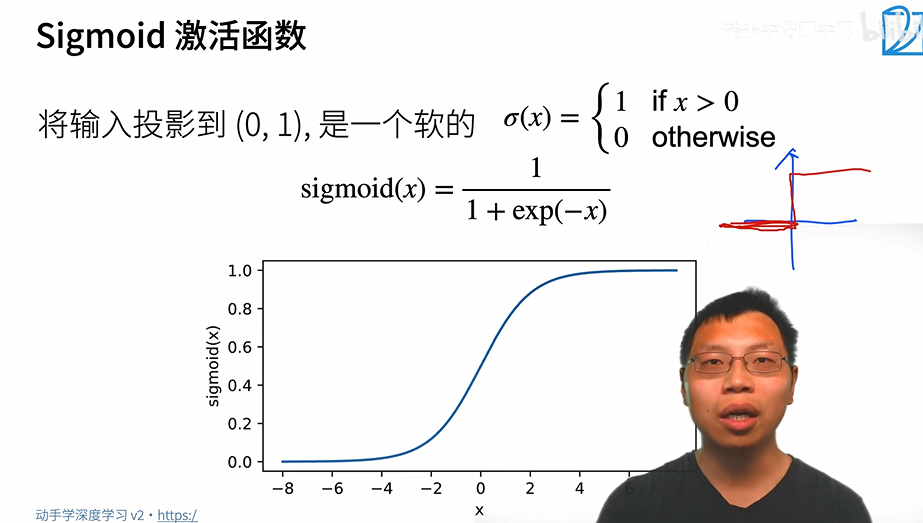
Tanh激活函数:
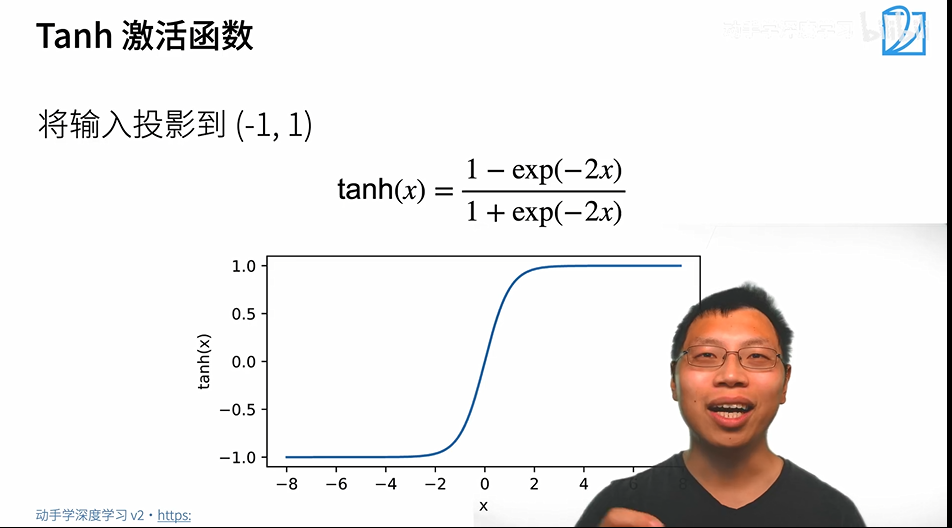
ReLU激活函数:
rectified linear unit,其实就是一个max而已,主要的好处就是算起来很快,不需要做指数运算。
指数运算是一个很贵的事情,在cpu上一次指数运算可能相当于上百次乘法运算,在GPU上好一点,但是还是很贵

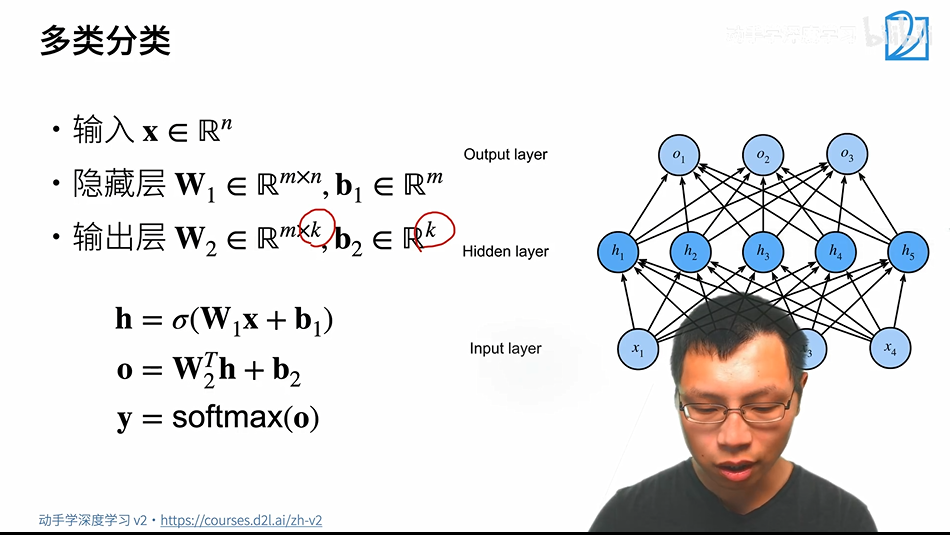
2.2.3 多类分类
定义和单类没有太大区别,就是输出层$W_2$变成了m*k,$b_2$变成了k维向量,然后对output做一次softmax
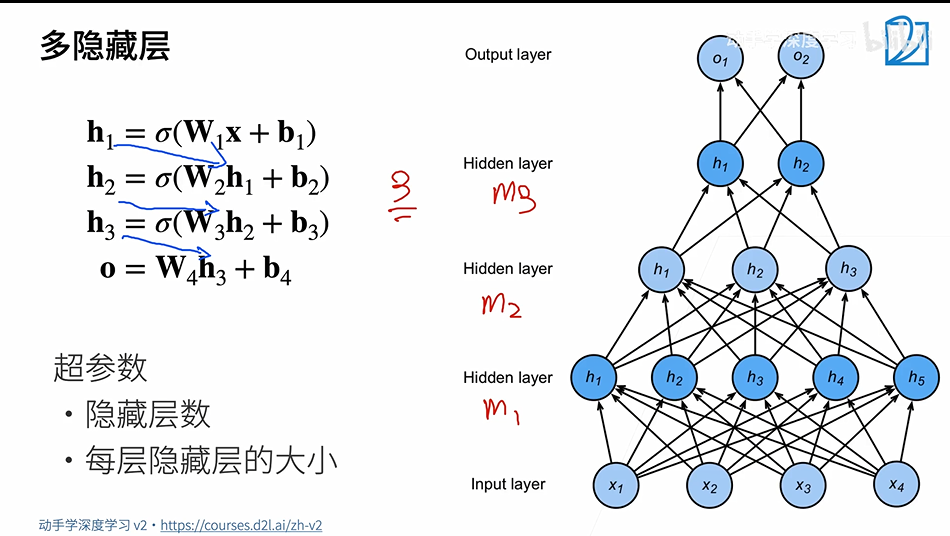
2.3 多隐藏层
每层的大小一般都是越来越小的(也可以先扩张再缩小),如果input的维度比较高可以使用多层隐藏层慢慢压缩。
2.4 总结
- 多层感知机使用隐藏层和激活函数来得到非线性模型
- 常用激活函数是Sigmoid,Tanh,ReLU(ReLU用的最多)
- 使用softmax来处理多类分类
- 超参数为隐藏层数,和各隐藏层大小
3.Q&A
- 1、神经网络中的一层网络到底是指什么?
- 一层通常是带有权重的一层,输入层不算做一层
- 2、数据的区域r怎么求,ρ怎么设定?实际中我们确实想找到数据分布的区域,可以找到吗?
- 收敛定理是统计学上的理论,数学上不去计算
- 3、XOR函数有什么应用呢?
- 没有什么用处,只是举个反例
- 4、是不是x轴是特征1,y轴是特征2,红蓝是他们的label?是这么对应每一条数据吗?所以感知机不能处理XOR?
- 对的,对于4个样本二维特征的样本都不能拟合,体现了感知机的局限性
- :label:5、为什么神经网络要增加隐藏层的层数,而不是神经元的个数?
- 网络可以采用层数少而神经元多的模型(矮胖),也可以使用层数多而神经元少的模型(高瘦)。但是,前者不好训练,后者容易训练。后者即是深度学习,前者是“浅度学习”。不好训练的原因就是需要一次拟合大量的神经元,一口气吃成胖子很难,而把一个复杂的东西分成多个步骤去学习就很容易了,所以叫“深度学习”
- 6、ReLU为什么管用,激活函数的本质是要做什么事?
- ReLU是一个非线性的函数,激活函数的本质是引入非线性型,不再去干别的事情
- 7、不同任务下的激活函数是不是都不一样?
- 激活函数的确定不是很重要,没有特殊情况就用ReLU。你可以去选,但是没有本质的区别